Ellis
Ellis
JR Ellis, October 1992
Department of Mathematics
University of Utah
A thesis submitted to the faculty in partial fulfillment of the requirements for the degree of Master of Science
This idea is applied to forming a complete ordered field with the
elements of the set of squares. After showing constructions for combining
the squares, pictures which show the group properties follow. Finally,
limit theory for an infinite sequence is shown graphically as a rectangular
prism is iteratively changed into a cube.
The intent of this paper is to suggest that teaching math in elementary
schools can be more conceptual and creative. By using approaches,
as outlined here, education can be more effective and stimulating
to young developing minds.
As I played with these ideas, I developed a simple system to see the
properties of the real number system by using squares in order to
visualize these properties. This thesis includes a video, which animates
the square root construction and proof, and demonstrates the advantages
and potential of computer graphics in education. The video was produced
in the Art and Film department, with the help, cooperation and resources
of the Mathematics and Education departments.
It is hoped that this idea will inspire a healthier approach to education
of people learning mathematics. High school students are routinely
taught how to factor the difference of two squares. However, the geometric
interpretation of this equation is completely ignored. When I realized
that the square of the hypotenuse of a right triangle equals the
sum of the square of its legs really referred to four-sided squares,
the square root construction followed easily. I was excited with the
awareness. I was also sad that I had plodded through algebra without
being exposed to its roots in geometry. I hope the pictures in this
presentation will bring the equations to life.
I would like to thank Professor Robert E. Barnhill from the University
of Utah for allowing me to pursue this path as a thesis and a film;
and Professor Bevan K. Youse from Emory University, for introducing
me to group theory and analysis and other recent private communications.
And also, I would like to thank Dr. Andrew Mitz from NIH for giving
me suggestions which helped me to write this thesis.
A complete ordered field is formed by using squares as the elements
of the set, with the operations of addition and multiplication. Constructions
for these operations are shown, as well as division and subtraction.
And there are pictures for properties like inverse, distributive,
and multiplicative associativity.
Finally, the square root construction is extended by applying the
procedure to an original iterative cube root construction. The limit
theory for this infinite sequence uses nothing more advanced than
an equation for the sum of a geometric progression. As with many of
the geometric assertions in this paper, the algebraic proof is also
included
The paper starts with an arithmetic application to the geometric interpretation
of the difference to two squares. This shortcut can be used in normal
arithmetic calculations.
17 * 23 = (20 - 3) * (20 + 3) = 20**2 - 3**2 = 400 - 9 = 391
If the squares from one to one hundred are already memorized then
two digit multiplication will be much faster. There is another advantage
because there are fewer numbers to keep track of than with regular
multiplication. The square may be computed with an arithmetic application
of the binomial theorem for
17**2 = (20 - 3)**2 = 20**2 + 2(-3)(20) + (-3)**2 = 400 - 120 + 9 = 289
The advantages of this technique maybe illustrated with another example.
Here the challenge is to solve the following multiplication problem
without using paper and pen:
24 * 26 = (25
Now we may forget 24 and 26 and
remember 25 and 1. Next 25**2 = 625.
And Finally, 625
The standard way to multiply 24 and 26 is to first multiply 26
* 4 = 104 and then 26 * 20 = 520.
And in order to add (104 + 520), there are more numbers to remember
at one time than the previous proposed shortcut.
Point 2: The midpoint of line segment b1 ( a2 is the
average of the length and width.
Point 3: The midpoint of line segment a2
Point 4: The intersection of a circle having its center at point 3 and radius
equal to line segment a3, with a circle having its cetner at point 2 and radius
equal to line segment b2
Line segment a4 represents the side of the square whose area equals that of the rectangle.
When the width of the rectangle is the unit width, the length of a4 is the square root of line
segment ab. To find the square root of a measure, start with a unit width rectangle having its
length equal to that measure. Then use this construction to change the rectangle into a square.
The side fo the square is the square root of the length of the rectangle.
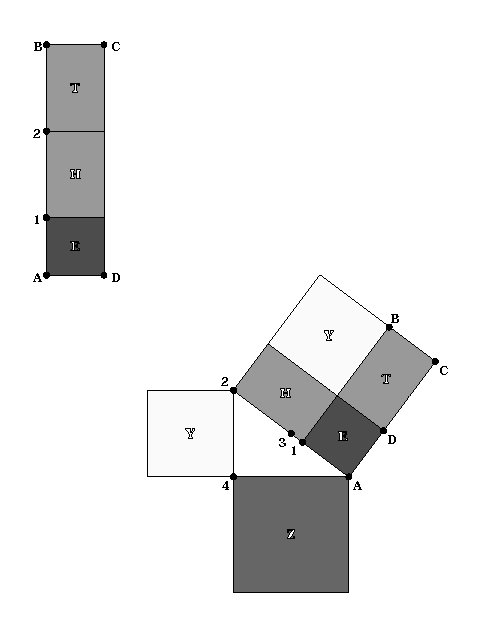
Geometrically, the construction is easy to
explain. Rectangle THE on the top left is equal in area to square
Z on the bottom right. In the first step of the construction,
rectangle THE is divided into 3 parts. Point 1 marks square
E, and Point 2 divides the remainder into 2 equal
rectangles: T and H.
Points A, B, 1, 2, 3, and 4 correspond
to the square root construction from the previous page.
In the second step, the bottom picture shows rectangle THE transformed
by separating rectangle T and attaching it to square E
as shown. Rectangle THE is now an irregular hexagon, and also
the difference of two squares. (AC and A2 are equivalent
since E is a square, and H and T are equivalent
rectangles.) Finally Square Z is resolved through the
subtraction construction already shown.
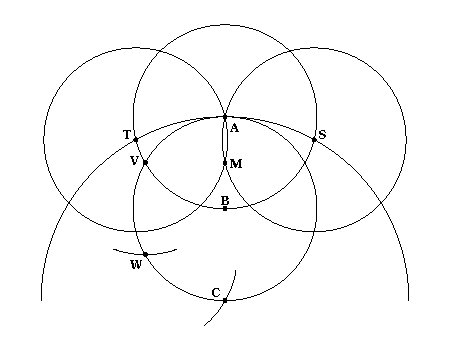
Here we are given the point P and the circle K
with center O. Construct the circle through P with center
O, and from P mark off the radius three times (points
Q, R, S) on the circumference, and also mark off
the distance ST = r.
Then PT = sqare root { 4p**2 -r**2 }.
Draw the circles about P and S with radius
PT, thus obtaining the point U. Draw the circle with
center U and radius PR = p [ square root { 3 } ] , thus obtaining
the points X and Y (in all, eight circles are necessary).
Given: OP = OQ = OR = OS =
PQ = QR = RS = p, UX = PR, UP = PT, OX = TS = r,
angle UOP is a right angle, X lies on the
circle (O, r).
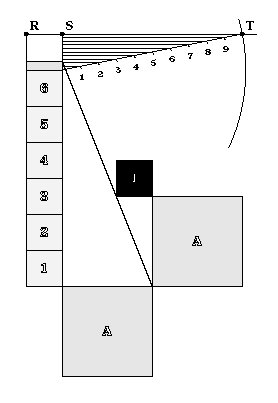
To measure a line, count off unit lengths as shown. Then proceed to
obtain the next significant digit from the remainder. Construct a
line ruler of ten arbitrary units, for base ten. The units may be
different than the unity square. Draw a circle using the length of
the ruler as radius and the center of the circle as the endpoint of
the last whole unit that fit into the length of the unit rectangle.
Find Point T where the circle intersects line RS.
Draw lines parallel to RS from each calibration point on the
ruler to obtain the next significant digit of the measure. Repeat
this procedure for the next significant digit. In this case, it would
be obscure to find that 6.25 is the measure of square A, because
the construction would be taking place in an area which is too small
to be practical.
This construction may be applied to measure the line on the side of
the square that was obtained in the square root construction.
The construction for the cube root works by changing a unit rectangular
prism into a cube. The starting rectangular prism has unit squares
on two opposite faces, while the other four are unit rectangles, having
length equal to a. This construction is iterative, producing
a sequence that converges to a cube with a side equal to the cube
root of a.
At each stage of the sequence, transform and mold the prism by constructing
a square from the unit rectangle. This transformation will retain
the area, while producing, once again, a rectangular prism where two
opposite faces are squares. Eventually, it approaches a cube.
The proof which is not shown uses limit theory of series and sequences
to show that transformation of the rectangular prism in this manner
does indeed converge to a cube. Limit theory may be used since the
set of squares with the operations of multiplication and addition
is isomorphic to the set of real numbers.
ABSTRACT
An original four point compass and straight-edge construction is proposed
for finding the square root of a line segment. The construction is
geometrically derived and illustrated as changing a rectangle into
a square in two stages. First, by turning the rectangle into the difference
of two squares; and second, by subtracting them.
ACKNOWLEDGMENT
I became exited when I discovered the square root construction that
will be shown in this paper. The concept came naturally as I thought
about the geometric interpretation of simple algebraic equations.
I was most amazed that I hadn't thought of it sooner. After spending
a lifetime in formal education classes, I hadn't really understood
the simple concepts of algebra and geometry that men have known for
thousands of years.
INTRODUCTION
This thesis offers an original basic four point paper construction
for square root by turning a rectangle into a square. The process
first transforms the rectangle into the difference of two squares,
so constructions and proofs for addition and subtraction of squares
are presented first. The complete construction is given, including
conceptualization and the proof. Also two compass-only procedures,
which can be used in three of the four steps of the square root construction,
are supplied so that the whole construction may be done with paper
and compass and without needing a straight-edge. Even a construction
to exact the measure of lines and squares is detailed, in order to
exact real numbers from the root square.
ARITHMETIC
Let's consider the arithmetic problem y multiplied by x.
Sometimes it is easier to change the problem into
a**2 - b**2,
where a = 1/2(x + y) and b = 1/2(x - y).
Let
a represent the average of x and y, while b
represents the deviation of x or y from this average,
or x - a. This is useful when the squares are easy to compute.
For example:
n = 2, (a + b)**2 = a**2 + 2ab + b**2. (sorry... picture missing )
SQUARE ADDITION
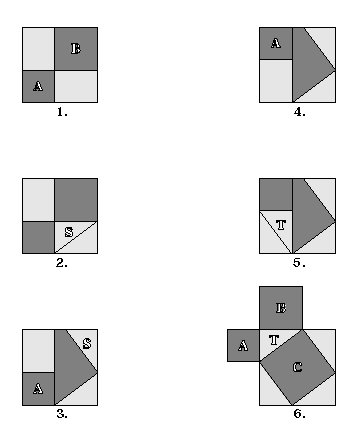
SQUARE ADDITION TESSELLATION
TRIGNOMETRIC DEFINITIONS
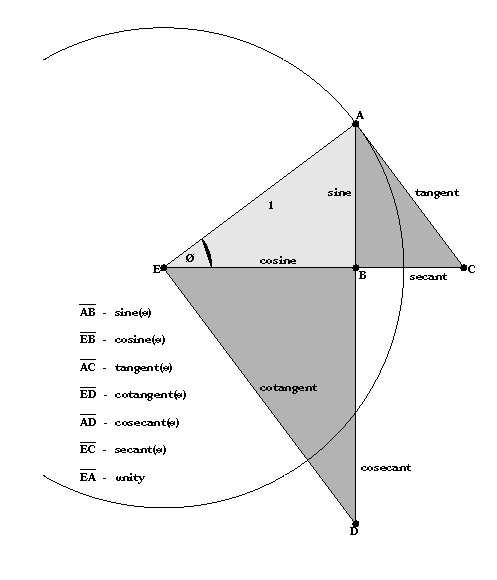
theta = arcsin AB
SQUARE SUBTRACTION
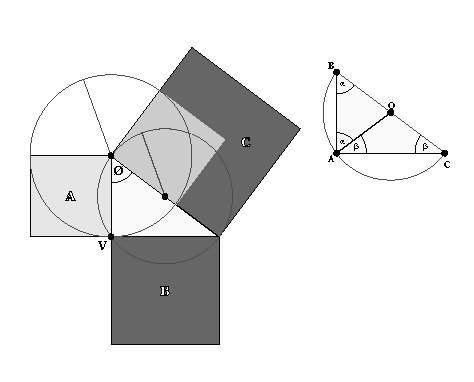
SQUARE ROOT CONSTRUCTION
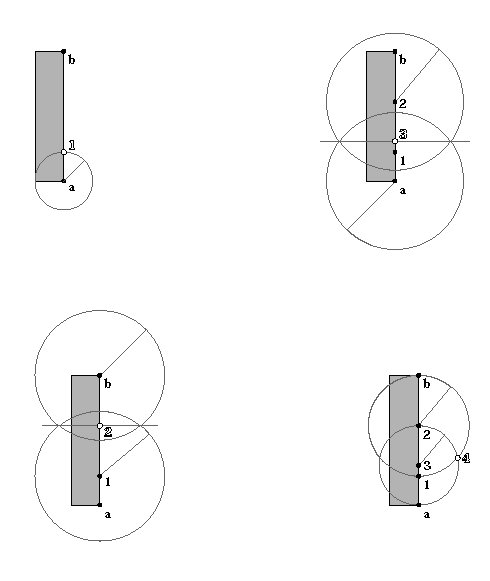
Point 1: The intersection of line segment ab with the circle having its
center at point a and radius equal to the side of the rectangle.
Geometric Proof
Compass-Only Construction of the Midpoint of a Line
Segment
Compass-Only Construction of the Intersection of a Circle
and a Line
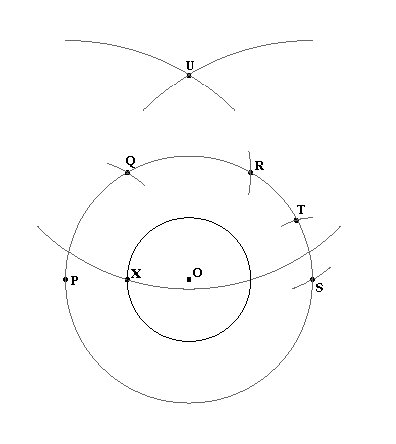
Proof of the Compass-Only Construction of the Intersection
of a Circle and a Line
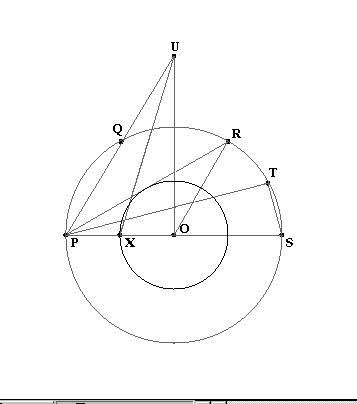
Proof
so line segment PR = p {square root [ 3 ] }
square root [p**2 + p**2 - 2(p)(p)cos{2pi / 3} ] = p {square root [ 3 ] }
SQUARE MULTIPLICATION
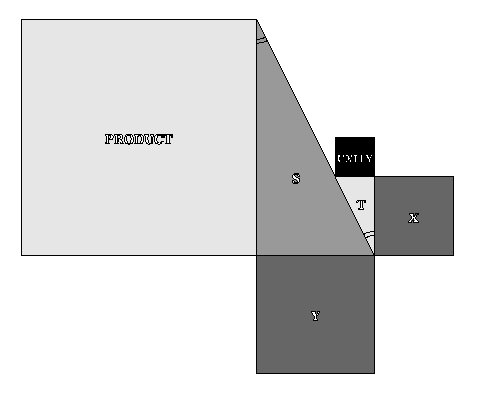
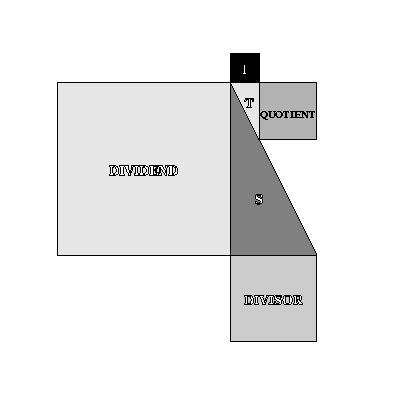
SQUARE DIVISION
SQUARE MEASURE
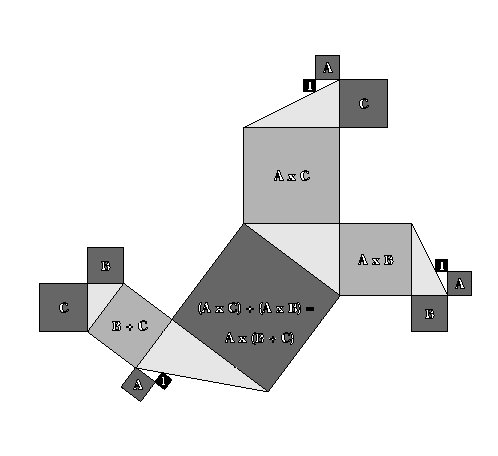
SQUARE DISTRIBUTIVE PROPERTY
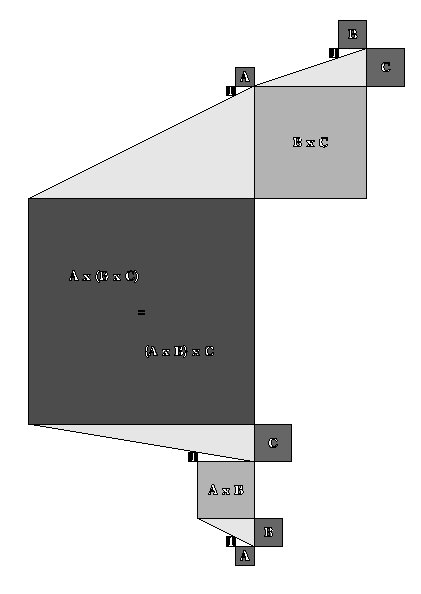
SQUARE MULTIPLICATIVE ASSOCIATIVE PROPERTY
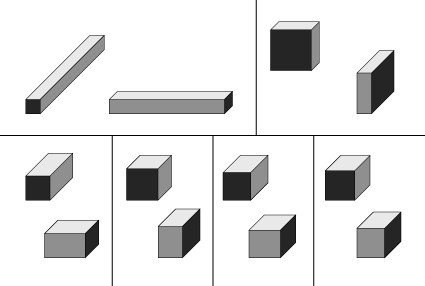
CUBE ROOT
